Recess #2: The Race to the Bottom, Then Back to the Top, Then Back to the Bottom, Then...
How much ground could you cover in a full day of skiing?
Ski Patrollers at the Park City ski resort in Utah recently won key demands and ended their strike against Vail Resorts. The strike itself unfolded over the tail end of the holidays, and this past week a group of tourists visiting the mountain filed a class action lawsuit against Vail Resorts alleging that the company did not disclose the full impacts of the strike on the mountain experience, and namely lift and trail closures. As it turns out, wealthy ski vacationers that can afford to pay thousands, or tens of thousands of dollars for a vacation over the holidays are also a somewhat litigious group.
But I think these plaintiffs are asking the wrong questions. They are wondering if, and how, they can get their money back, not “How can I make up my lost runs on the mountain as fast as humanly possible?” How much ground can I cover in a single day of skiing to make up for the days with fewer runs? Thankfully, we don’t even have to go outside to answer these questions— we can use relatively simple math to get close!
We’re going to create an equation that will govern the average speed of a skier going downhill and going uphill on some form of lift. Hopefully by the end of writing I’ll have come up with a clever name for this equation, so stay tuned. We’ll then do some quick sleuthing to figure out how this math applies to Park City and pick a route to try to maximize the amount of skiing done in a single day. Remember, my goal is to provide answer quickly, so I will be avoiding the pitfalls (tree wells?) that might make the analysis more nuanced and accurate, but require additional time.
Math, Part 1: Creating Math
First, let’s select total distance covered while skiing (lifts don’t count) as the variable to optimize and estimate. We can approximate the total distance as the hypotenuse of the triangle formed by the vertical descent (“v”), and the horizontal distance (“h”). We also need to figure out the independent variables, so we’ll need average speed uphill and downhill, along with total activity time to calculate total distance covered. Speed on the lift up and on the skis down will have their own set of inputs. Let’s look at the downhill first!
With downhill skiing, we will chose to avoid our first pitfall. We could get all nuanced by estimating the aerodynamic drag and sliding friction of a skier at different slope angles, and use a lot of complicated math to calculate the average speed. OR, we could opt for the easier path and estimate average speed by putting reference points on a spectrum and guessing where the average skier falls between: a kid doing pizza a continuous pizza stop (4 MPH), Lindsey Vonn’s recent top speed during a Super G race (68 MPH), and the terminal velocity of a human falling through air (120 MPH):
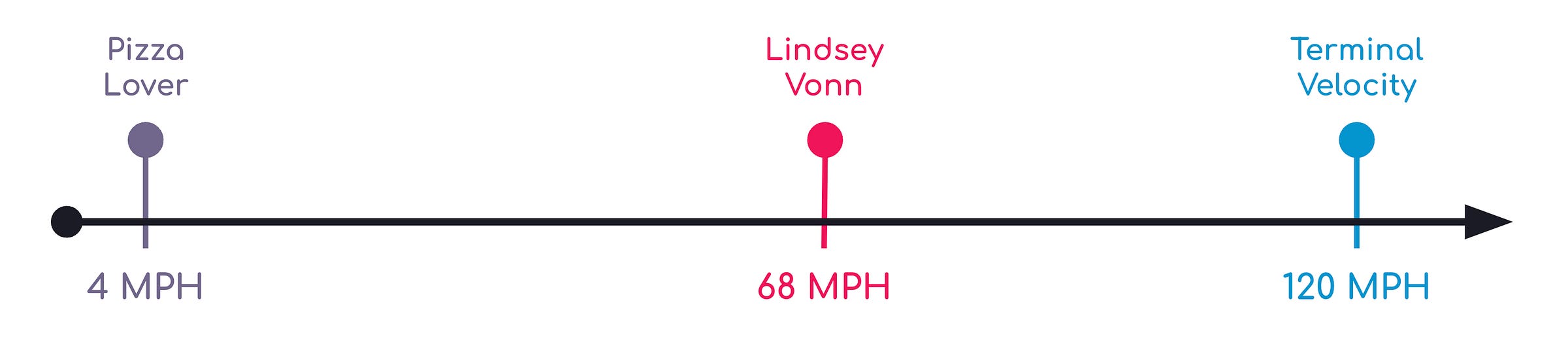
The good news is that with rare exception almost every single skier and snowboarded falls somewhere between Pizza Lover and Lindsey Vonn when it comes to average speed. So, to streamline the math, let’s collapse the average speed into one constant along with a couple coefficients to modify it: Lindsey’s average speed on Super G (68) is the constant, and we’ll include two coefficients. First, the speed coefficient (“S”) is the estimated percent of Lindsey Vonn’s max speed is achievable on an average run expressed as a decimal (i.e. 0-1). Second, the delusion coefficient (“D”) applies based the overconfidence of the skier, and is a number between 1-2— the more delusional the skier, the higher the value. When we include the average speed as the hypotenuse distance/time, we get an average downhill speed of:
To isolate the time it takes go down a run, we rearrange and simplify into:
The Delusion factor (“D”) is now in the numerator where it belongs.
For getting back up the mountain, calculating time is a bit simpler. We just need a type of lift to estimate the top speed (“T”), and a coefficient that governs how close to this top speed you actually achieve on average— a load/unload spill coefficient (“Sp”) that might be higher for shorter lifts, especially if lines are forming. A gondola typically achieves a to speed of ~13 MPH, while a fixed-grip and detachable chairlift achieve ~5 MPH and ~11 MPH respectively. Pulling this info together, you get the following simple equation for uphill speed:
Isolated to time on lift, we end up with:
Now we can add this to the time down the run to get a total time per loop! Note that I’m assuming we’re going up and down the same distance in this combined and simplified equation:
I’ve gone about this a bit circuitously in part because it’s fun to see how even basic equations of motion get simplified, but the party doesn’t stop here! If we wanted to see how many loops we can do in a day, we would take the total hours of operation (“H”), and divide it by the Time Per Loop. To then get total distance covered in a day, we’ll then multiple this # of loops by the distance of each loop, the sqrt(h^2 + v^2). Combining these two steps generates the following equation:
Now we can cancel out the distance per lap, sqrt(h^2 + v^2), and end up with a pretty elegant equation governing the total distance covered in a day!
Some of the beauty here is that the the distance of the run is completely irrelevant in a theoretical equation like this (unless it’s zero), unless it is affecting the time spent in line or the Spill coefficient!
Math, Part 2: Using Math
Park City’s normal lift operating hours are 9am-4pm, a total of 7 hours per day (i.e. H = 7). In taking a look at the resort map for the firs time, the Super Condor express and the Apex Ridge trail running beneath it seem a prime candidate for going as fast as possible. The lift is a long detachable chair (T = 11), and mostly services advanced terrain, so the Spill factor might be close to ~0.9 (Sp = 0.9). The run is a straight blue square the whole way down, and while I’ve never skied Park City, I have to imagine this run as SLOW signs all over it if it’s like other intermediate bombers I’ve seen:
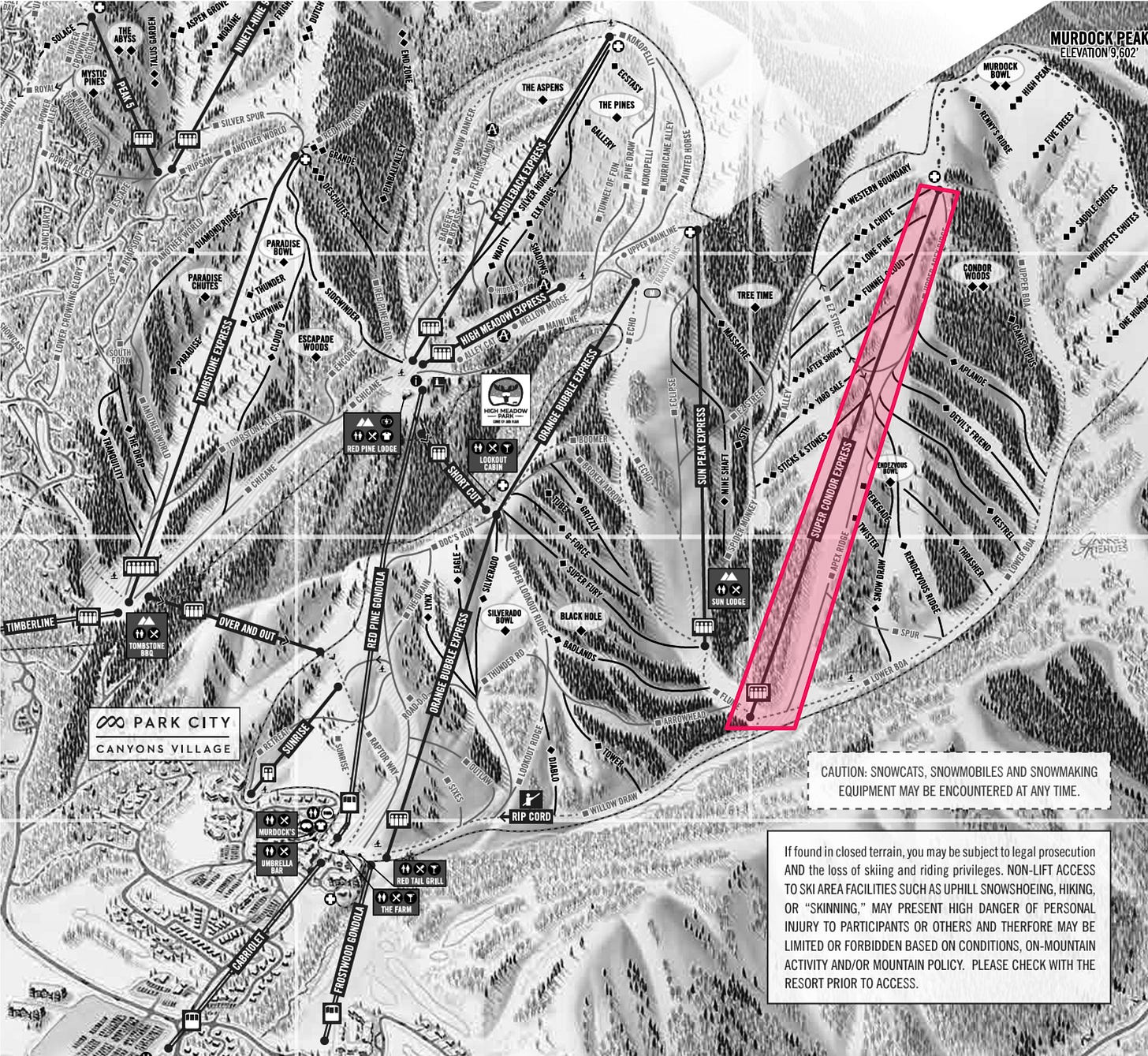
I will serve as the downhill skier average speed estimator Guinea pig. I think I’m probably closest to Lindsey Vonn’s speed than someone doing pizza, which automatically means my delusion factor is quite high, perhaps even a 1.5 out of 2 (D = 1.5). However, I think that I can probably only ski roughly as half as fast on Lindsey Vonn on an average run (S = 0.5). The combination of these implies my average downhill speed is ~17MPH, which is probably reasonable. Plugging these values into our calculator yields the following:
If you are curious, I’d be spending about 3/4 of my time on the lift relative to the runs in this calculation (yuk). However, assuming Park City is open half the year on a good winter, you could cover nearly 9,000 miles in one ski season! For reference a pizza skier is covering roughly 19 miles in a single day, but is spending 1.5x time skiing as opposed to riding the lift. Someone descending the mountain at terminal velocity covers about 64 miles in a day, but spends over 90% of their day on a ski lift as opposed to skiing! That does not sound like time well spend to me…
So what did we truly learn here besides the fact that you can feasibly ski a ton of distance in a single day if you really tried, and coming up with completely inane equations to make estimations is quite fun? Well, maybe just that skiing at the terminal velocity of a human falling through the air isn’t as good of a deal as its cracked up to be— at least when it comes to skiing.
P.S. I finally decided on a name for this calculation: The Après Equation. Ironically I forgot to factor après-ski this into the equation itself, so you can just cut all the values in half up above— we all quit by 1pm.




